Dernière mise à jour : 25/07/2019 (Chiffrement par décalage: code César)

Pourquoi cette page ?

Dernière mise à jour le : 31/8/2017

Cela fait longtemps que je fais de la programmation (depuis le début des années 1980 en fait). J'ai donc connu l'informatique à ses tous débuts (enfin presque) et j'ai pratiqué divers langages de programmation depuis l'assembleur jusqu'à des langages plus évolués (basic, fortran, pascal, VBA,...). Tout cela appartient au passé, mais même si les langages de programmation ont évolué, il est une constante dans la programmation, l'algorithmique. D'ailleurs le mot "algorithme" vient du nom latinisé du mathématicien Al-Khawarizmi qui est né en Perse vers 780. Mais qu'est-ce qu'un algorithme ? Un algorithme est une suite finie et non ambiguë d’opérations ou d'instructions permettant de résoudre un problème ou d'obtenir un résultat. Un algorithme permet donc de structurer la pensée et implique un ordre logique des opérations. C'est pour cela que faire de l'algorithmique peut développer la méthodologie et le raisonnement quel que soit l'âge de la personne qui s'y met. Les nouveaux programmes scolaires mis en place à compter de la rentrée 2016 font également la part belle à tout ce qui est algorithmique, et ce dès le cycle 2. La meilleure façon, à mon sens, de s'initier à l'informatique est de lire et refaire des programmes simples au début,en comprenant bien les instructions (modifier légèrement les programmes pour constater concrètement ce que cela donne). Cette rubrique est donc destinée à tout public (enfant ou adulte) désirant entrer dans le monde de la programmation à travers des problèmes simples. Mais avant de commencer,

il sera nécessaire de vous procurer quelques outils (gratuits).

Les outils indispensables

Pour s'initier à l'algorithmique, il existe un logiciel fantastique et gratuit (ce qui ne gâche rien). Il sera utile pour tester les algorithmes proposés dans cette page.

Télécharger Algobox

Pour la partie programmation, je vous propose de le faire en langage Python. Python est un langage puissant, riche en possibilités et très prisé des informaticiens à l'heure actuelle. Python est un langage de programmation objet. Il favorise la programmation impérative structurée, fonctionnelle et orientée objet. Le langage Python est placé sous une licence libre. Il est conçu pour optimiser la productivité des programmeurs en offrant des outils de haut niveau et une syntaxe simple à utiliser. Il est également apprécié par les pédagogues qui y trouvent un langage où la syntaxe, clairement séparée des mécanismes de bas niveau, permet une initiation aisée aux concepts de base de la programmation.

Télécharger Python

Le dernier outil indispensable dans cette rubrique est un tableur. Un tableur offre des possibilités que peu imaginent. Il peut certes faire des calculs répétés et infinis mais il permet parfois de surpasser les langages de programmation pour certaines applications. Il sera intéressant dans cette rubrique de comparer la recherche de la solution à un problème avec un tableur ou avec un programme en Python. Deux versions de tableur sont intéressantes : Excel de la suite Office qui est payant et Open Office Calc qui lui est gratuit.

Télécharger la suite Open Office

Pour télécharger les programmes et algorithmes qui suivent: click droit et "Enregistrer la cible sous ...

Code César: chiffrement par décalage

En cryptographie, le chiffrement par décalage, aussi connu comme le chiffre de César ou le code de César, est une méthode de chiffrement très simple utilisée par Jules César dans ses correspondances secrètes (d'où le nom). Le texte chiffré s'obtient en remplaçant chaque lettre du texte clair original par une lettre à distance fixe, toujours du même côté, dans l'ordre de l'alphabet. Pour les dernières lettres (dans le cas d'un décalage à droite), on reprend au début.

Ici, je vous propose d'élargir ce principe en réalisant un système de cryptage utilisant les codes ASCII des caractères alphabétiques, numériques et ponctuation. Cela permettra d'éviter de revenir au début si l'on atteint le 26ème caractère et cela simplifiera d'autant l'algorithme. Pour cela nous utiliserons les codes ASCII.

L'American Standard Code for Information Interchange (Code américain normalisé pour l'échange d'information), plus connu sous l'acronyme ASCII ([aski]), est une norme informatique de codage de caractères apparue dans les années 1960. C'est la norme de codage de caractères la plus influente à ce jour. ASCII définit 128 codes à 7 bits, comprenant 95 caractères imprimables : les chiffres arabes de 0 à 9, les lettres minuscules et capitales de A à Z, et des symboles mathématiques et de ponctuation.(Wikipédia)
Description de l'algorithme:
- Demander à l'utilisateur de rentrer le message à coder.
- Entrer le code ou clé (valeur du décalage).
- Décomposer le message en caractères séparés.
-Pour chaque caractère ajouter le code (après avoir fait un test si le code ASCII est un espace (code ASCII = 32), auquel cas on n'ajoute pas le code.
- Réassembler le message de sortie.

ALGORITHME du CODE CÉSAR

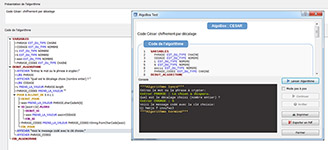
Cliquer sur l'image pour agrandir

Faire un clic-droit et utiliser l'option "enregistrer sous" pour télécharger le fichier.

PROGRAMME PYTHON du CODE CÉSAR

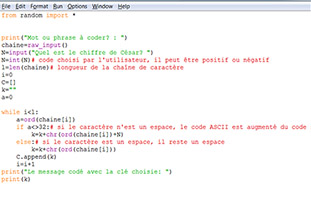
Cliquer sur l'image pour agrandir

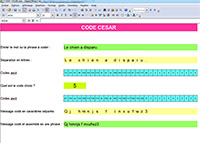
Cliquer sur l'image pour agrandir

Jeu du nombre à deviner

(Un petit jeu très sympa et très facile à programmer pour le début)Principe du jeu: Deviner en 7 essais maximum un nombre N (choisi par l'ordinateur) entre 1 et 100. On indique chaque fois si le nombre proposé est trop grand ou trop petit. La fonction random donne un nombre entre 0 et 1. Il faudra donc multiplier ce nombre par 100, prendre la partie entière "round" (arrondi en anglais) avec ALGO et "int" (integer en anglais) avec Python et ajouter 1 (sinon on s'arrête à 99).

ALGORITHME du NOMBRE A DEVINER

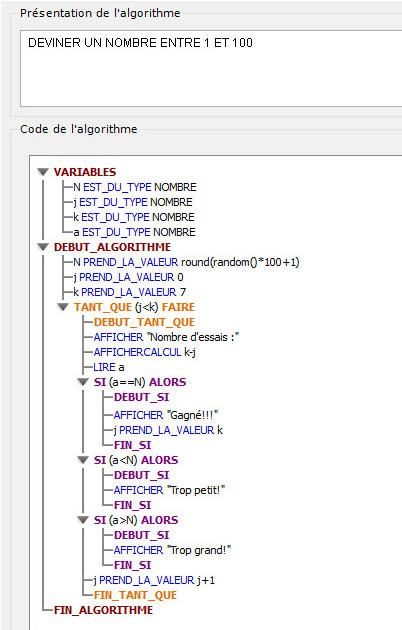
Cliquer sur l'image pour agrandir

Faire un clic-droit et utiliser l'option "enregistrer sous" pour télécharger le fichier.

PROGRAMME PYTHON du NOMBRE A DEVINER

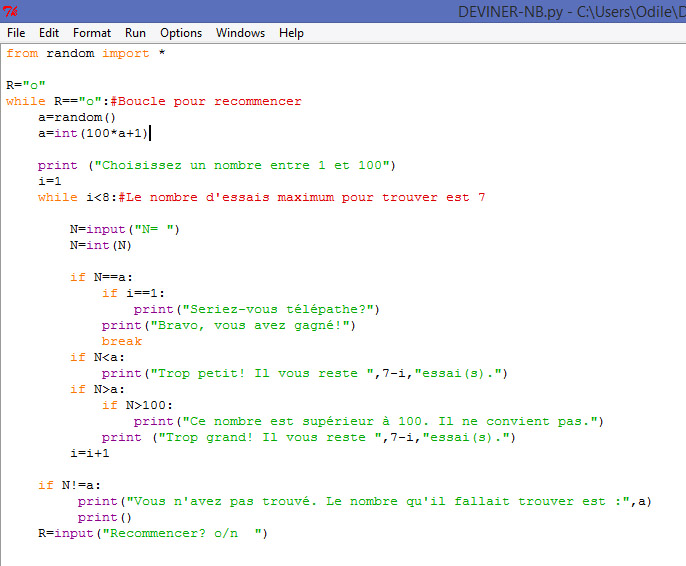
Cliquer sur l'image pour agrandir

 

Jeu du lièvre et de la tortue

Principe du jeu : À chaque tour, on lance un dé. Si le 6 sort, alors le lièvre gagne la partie, sinon la tortue avance d’une case. La tortue gagne quand elle a avancé 6 fois.

ALGORITHME du JEU DU LIÈVRE ET DE LA TORTUE

Pour générer un nombre aléatoire entre 1 et 6 avec des valeurs entières, on utilise la fonction ALGOBOX_ALEA_ENT(1,6). La partie se joue en 6 coups, une boucle TANT QUE la variable "tour" est inférieure ou égale à 6 est donc utilisée. Si le 6 sort, le lièvre gagne et l'on sort de la boucle. A chaque lancer de dé on affiche la valeur du dé et le résultat.

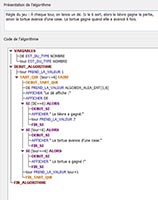
Cliquer sur l'image pour agrandir

Faire un clic-droit et utiliser l'option "enregistrer sous" pour télécharger le fichier.

PROGRAMME PYTHON du JEU DU LIÈVRE ET DE LA TORTUE

Avec Python, la sortie de la boucle, si le lièvre gagne, se fait simplement avec un "break".

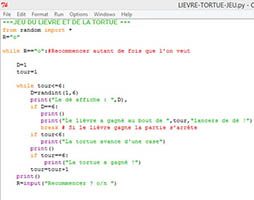
Cliquer sur l'image pour agrandir

Multiples de 9

Principe: Trouver les multiples de 9 inférieurs à un nombre N choisi par l'utilisateur. Quel intérêt me direz-vous ? Cela peut être utile en mathématiques. De plus on pourra changer le 9 par 2, 3, 4,... et constater de manière empirique les critères de divisibilité (la théorie se fera en TS avec les congruences). De manière plus élégante on pourra mettre le diviseur 9 sous forme de variable à entrer au début.
Description de l'algorithme: Pour chaque nombre inférieur à N en partant de 1 on regarde le reste de la division euclidienne de ce nombre par 9. Il existe la fonction % (Algo et Python) qui calcule le reste de la division euclidienne. Quand ce reste est égal à 0 on ajoute le nombre divisible par 9 à la table D[]. Le rajout à la table se fait avec la fonction D.append(k) et on incrémente k de 1 (ainsi de suite jusqu'à N).
ALGORITHME des MULTIPLES DE 9

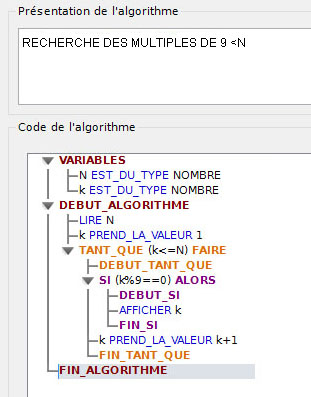
Cliquer sur l'image pour agrandir

Faire un clic-droit et utiliser l'option "enregistrer sous" pour télécharger le fichier.

PROGRAMME PYTHON des MULTIPLES DE 9

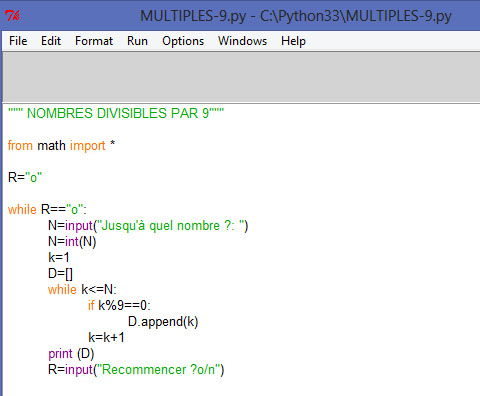
Cliquer sur l'image pour agrandir

Diviseurs d'un nombre

Principe: Trouver tous les diviseurs un nombre N choisi par l'utilisateur et les mettre dans un tableau. La résolution de ce problème est faite ici avec ALGO, Python et Open Office Calc.

Description de l'algorithme: Chercher le reste de la division euclidienne du nombre N par tous les nombres k inférieurs à N/2(inutile d'aller plus loin). Chaque fois que le reste est égal à 0, le nombre k est mis dans le tableau. Le programme indique si le nombre est premier.

ALGORITHME des DIVISEURS D'UN NOMBRE

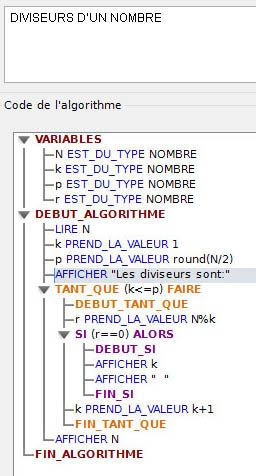
Cliquer sur l'image pour agrandir

Faire un clic-droit et utiliser l'option "enregistrer sous" pour télécharger le fichier.

PROGRAMME PYTHON des DIVISEURS D'UN NOMBRE

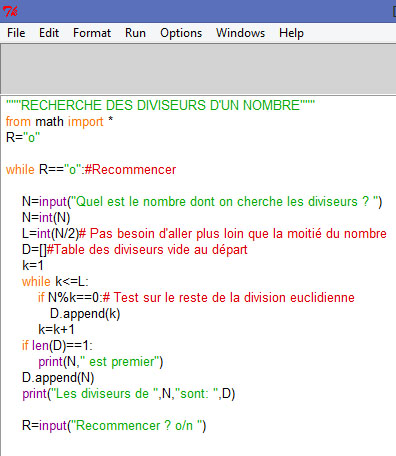
Cliquer sur l'image pour agrandir

DIVISEURS D'UN NOMBRE avec OPEN OFFICE CALC

L'inconvénient (qui est dans certains cas un avantage) est que tous les calculs doivent s'afficher dans les cellules du tableur. Le nombre dont on cherche les diviseurs est entré dans la case bleue. Tous les diviseurs de 1 à 1000 ici (mais il est très facile d'aller beaucoup plus loin en propageant les formules) sont affichés simplement avec la formule "=ligne()" dans la première ligne. Dans l'exemple ici, je commence à la ligne 6 donc la formule est "ligne()-5".

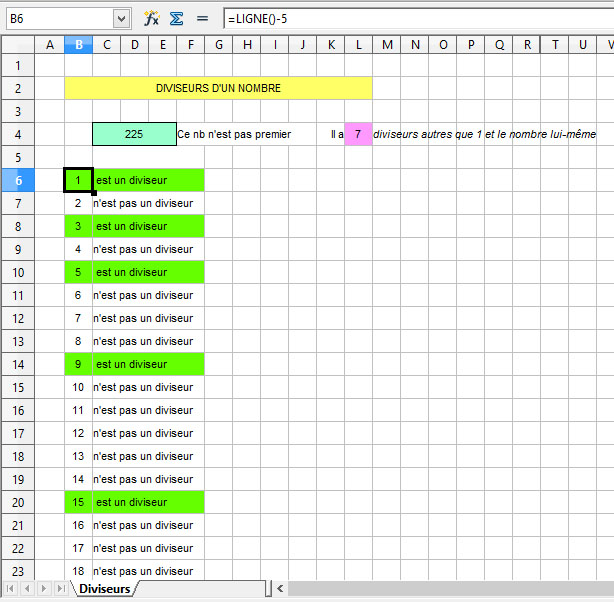
Le tableur permet de calculer le reste de la division euclidienne de 2 nombres, avec la formule "MOD( ; )". La division est donc effectuée à côté de chaque diviseur. Avec un formatage conditionnel on peut faire afficher en vert les diviseurs (voir la saisie d'écran suivante). Les diviseurs sont ensuite comptés (cellule rose) avec la formule "NB.SI( : ;" est un diviseur")-2". On enlève 2 car le 1 et le nombre lui-même sont des diviseurs. (voir saisie d'écran 3)

 

Carrés parfaits

En mathématiques, un carré parfait est le carré d'un entier.

Principe: Trouver tous les nombres inférieurs à un nombre N choisi par l'utilisateur et qui sont des carrés parfaits. Le même exercice avec une variante: chercher les nombres qui sont des cubes parfaits.

Description de l'algorithme: calculer le carré des nombres tant qu'il est inférieur au nombre N choisi par l'utilisateur. Afficher les carrés parfaits.

ALGORITHME des CARRÉS PARFAITS

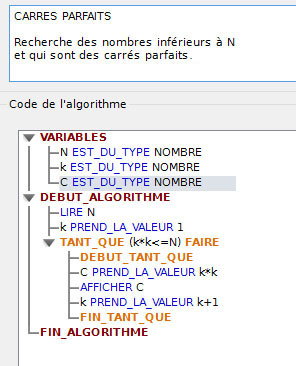
Cliquer sur l'image pour agrandir

Faire un clic-droit et utiliser l'option "enregistrer sous" pour télécharger le fichier.

PROGRAMME PYTHON des CARRÉS PARFAITS

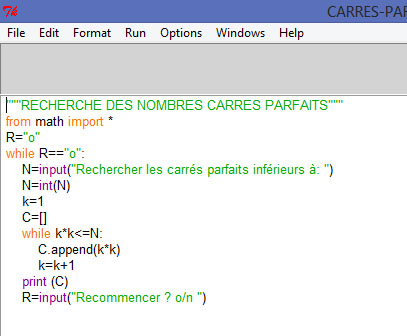
Cliquer sur l'image pour agrandir

Nombres premiers

Un nombre premier est un entier naturel qui admet exactement deux diviseurs distincts entiers et positifs (qui sont alors 1 et lui-même). Ainsi, 1 n'est pas premier car il n'a qu'un seul diviseur entier positif ; 0 non plus car il est divisible par tous les entiers positifs.

Principe: Trouver tous les nombres inférieurs à un nombre N choisi par l'utilisateur et qui sont des nombres premiers.

Description de l'algorithme: Au départ la liste L contient 2, le premier nombre premier. Le nombre suivant est divisé (division euclidienne) par tous les nombres premiers déjà dans la liste. Si le reste de chacune des divisions est différent de 0, le nombre est premier, il est alors rajouté à la liste.

ALGORITHME des NOMBRES PREMIERS

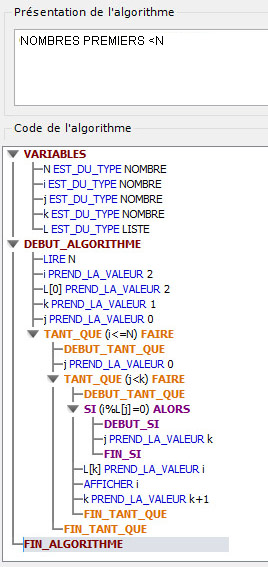
Cliquer sur l'image pour agrandir

Faire un clic-droit et utiliser l'option "enregistrer sous" pour télécharger le fichier.

PROGRAMME PYTHON des NOMBRES PREMIERS

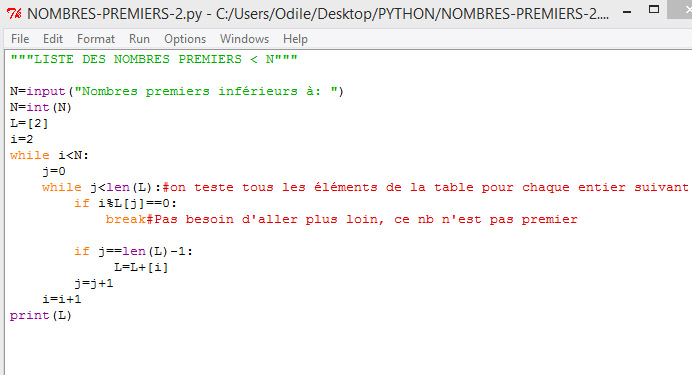
Cliquer sur l'image pour agrandir

PGCD de deux nombres

Le plus grand commun diviseur, abrégé en général PGCD, de deux nombres entiers naturels non nuls est le plus grand entier qui divise simultanément ces deux entiers. Par exemple le PGCD de 20 et 30 est 10. En effet, leurs diviseurs communs sont 1, 2, 5 et 10. Le plus grand nombre étant 10. Lorsque deux nombres n'admettent que 1 comme diviseur commun, on dit que ces deux nombres sont premiers entre eux.

Principe: Trouver le PGCD de deux nombres choisis par l'utilisateur suivant l'algorithme d'Euclide. Attention dans l'algorithme et le programme proposés ci-dessus, le nombre le plus grand doit être entré le premier. La (petite) modification du programme pourra être faite par l'utilisateur avec la fonction MAX(,),pour pouvoir rentrer les nombres dans un ordre quelconque.

Description de l'algorithme: L'algorithme d'Euclide, consiste à effectuer une suite de divisions euclidiennes: On effectue la division euclidienne de a par b et on note r le reste. Ensuite, b devient a et r devient b et on recommence: on effectue la division euclidienne de a par b et on note r le reste. Et on continue ainsi de suite jusqu'à ce qu'une division donne un reste égal à 0. Dans cet algorithme le PGCD est le dernier reste non nul.
L'algorithme indiquera également si les deux nombres proposés sont premiers entre eux.

ALGORITHME du PGCD

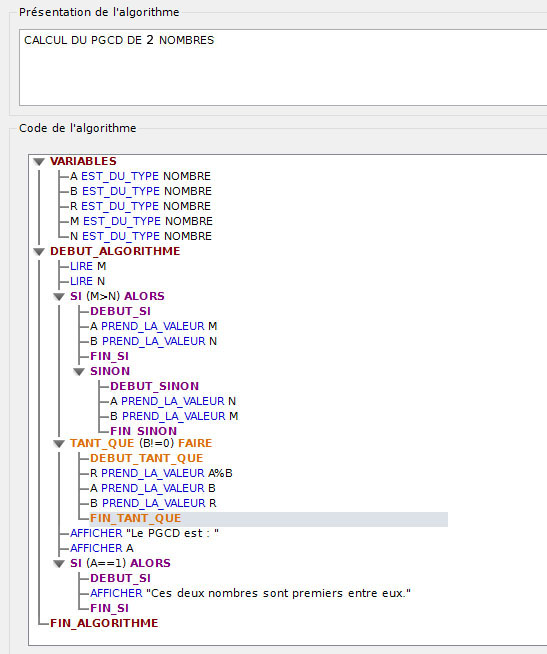
Cliquer sur l'image pour agrandir

Faire un clic-droit et utiliser l'option "enregistrer sous" pour télécharger le fichier.

PROGRAMME PYTHON du PGCD

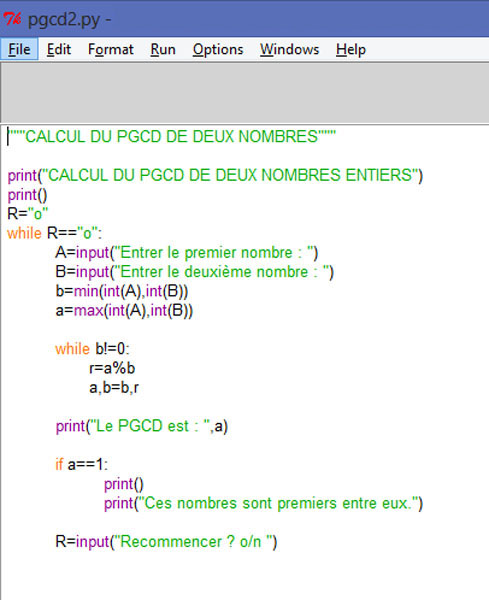
Cliquer sur l'image pour agrandir

Suite de Fibonacci

Principe: La suite de Fibonacci est une suite d'entiers dans laquelle chaque terme est la somme des deux termes qui le précèdent. Elle commence généralement par les termes 1 et 1 et ses premiers termes sont : 1, 1, 2, 3, 5, 8, 13, 21, etc. Elle doit son nom à Leonardo Fibonacci qui, dans un problème récréatif, décrit la croissance d'une population de lapins : « Un homme met un couple de lapins dans un lieu isolé de tous les côtés par un mur. Combien de couples obtient-on en un an si chaque couple engendre tous les mois un nouveau couple à compter du troisième mois de son existence ? » Cette suite est fortement liée au nombre d'or. Le nombre d'or est un nombre étonnant, mystérieux et magique pour avoir fait parler de lui depuis la plus haute antiquité dans de nombreux domaines tels que la géométrie, l’architecture, la peinture, la nature, … Il serait une expression d’harmonie et d’esthétique dans les arts ! Ce nombre intervient dans l'expression du terme général de la suite: les quotients de deux termes consécutifs de la suite de Fibonacci sont les meilleures approximations du nombre d'or. La résolution de ce problème est faite ici avec ALGO, Python et Open Office Calc.

Description de l'algorithme: L'utilisateur choisit le nombre de termes de la suite à calculer et afficher. Le rapport des deux derniers termes comme approximation du nombre d'or est également calculé et affiché.

ALGORITHME - SUITE de FIBONACCI

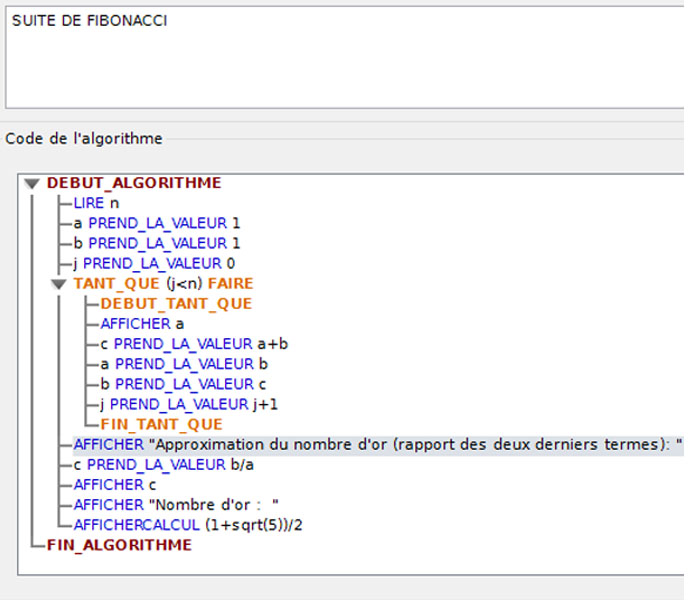
Cliquer sur l'image pour agrandir

Faire un clic-droit et utiliser l'option "enregistrer sous" pour télécharger le fichier.

PROGRAMME PYTHON - SUITE de FIBONACCI

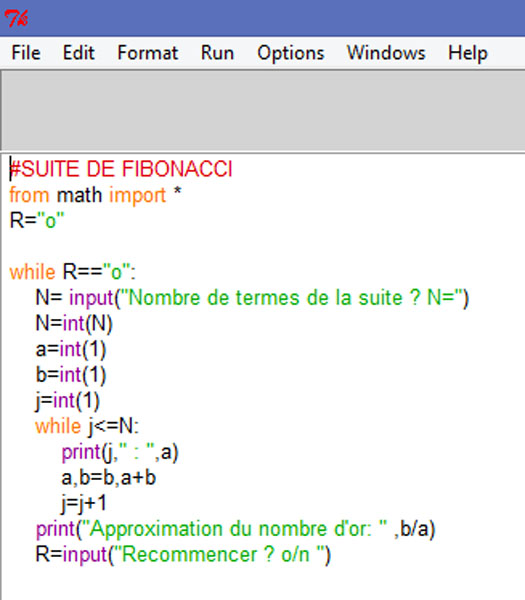
Cliquer sur l'image pour agrandir

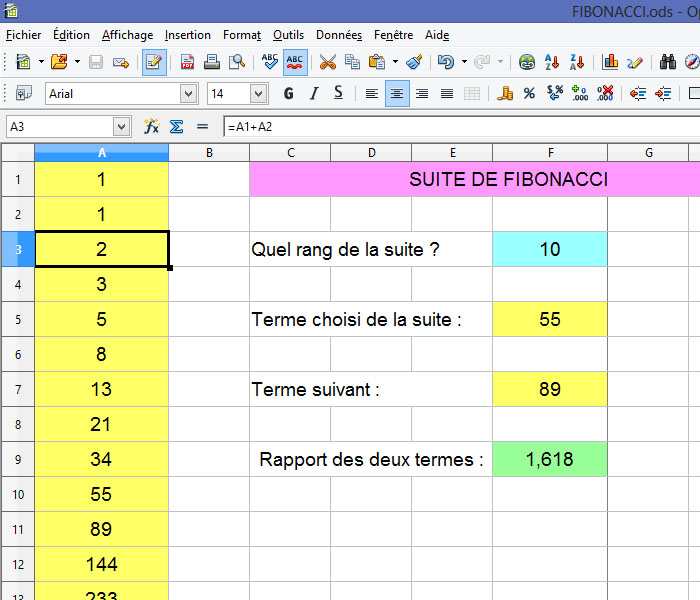
SUITE DE FIBONACCI avec OPEN OFFICE CALC

La résolution du problème avec Open Office Calc est très simple. Dans un premier temps; on entre 1 dans A1 et A2. Dans A3 on fait la somme des deux et on propage la formule (10000 termes dans l'exemple proposé).

Cliquer sur l'image pour agrandir L'utilisateur entre le terme de la suite qu'il veut voir. Celui-ci s'affiche dans la case jaune dessous, avec la formule dans l'exemple ici INDEX(A1:A10000;F3 ) (image suivante). Le rapport des deux derniers termes est affiché.

Tables de multiplication

Principe: Puisqu'il faut bien passer par l'apprentissage des tables de multiplication autant faire son propre exerciseur pour moins souffrir. Un séquence de 10 multiplications est proposée à l'utilisateur. Cet exerciseur est proposé ici avec ALGO, Python et Open Office Calc.
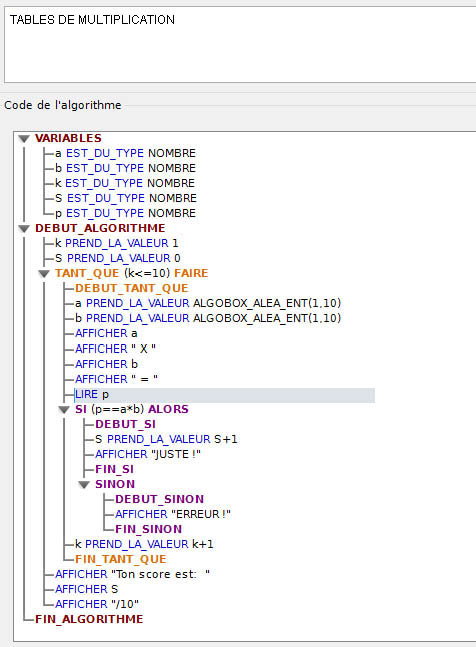
Description de l'algorithme: Il faudra prévoir une boucle de 1 à 10. Deux nombres aléatoires entre 1 et 10 sont choisis à chacune des boucles. Le score sur 10 est affiché à la fin de la séquence.
ALGORITHME - TABLES de MULTIPLICATION
Sous ALGOBOX, c'est la fonction ALGOBOX_ALEA_ENT(1,10) qui permet de générer un nombre aléatoire entre 1 et 10.

Cliquer sur l'image pour agrandir

Faire un clic-droit et utiliser l'option "enregistrer sous" pour télécharger le fichier.

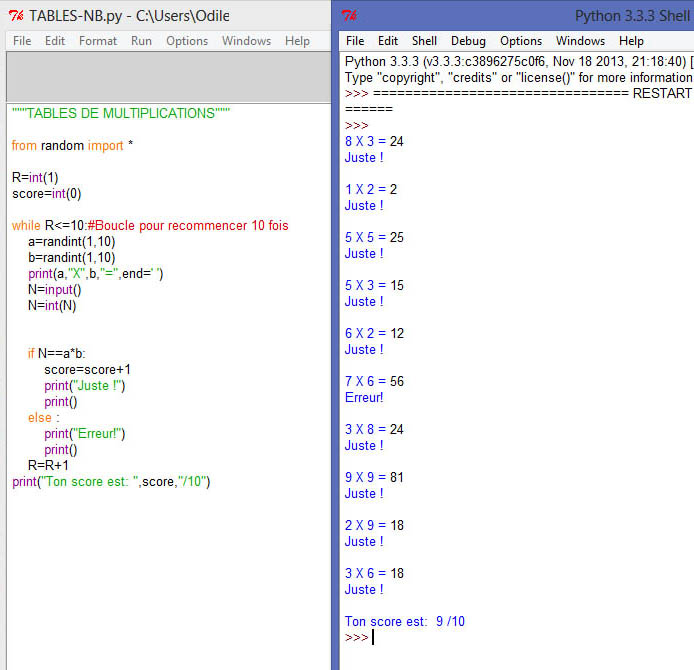
PROGRAMME PYTHON - TABLES de MULTIPLICATION

Sous Python, c'est la fonction randint(1,10) qui permet de générer un nombre aléatoire entre 1 et 10.

Cliquer sur l'image pour agrandir

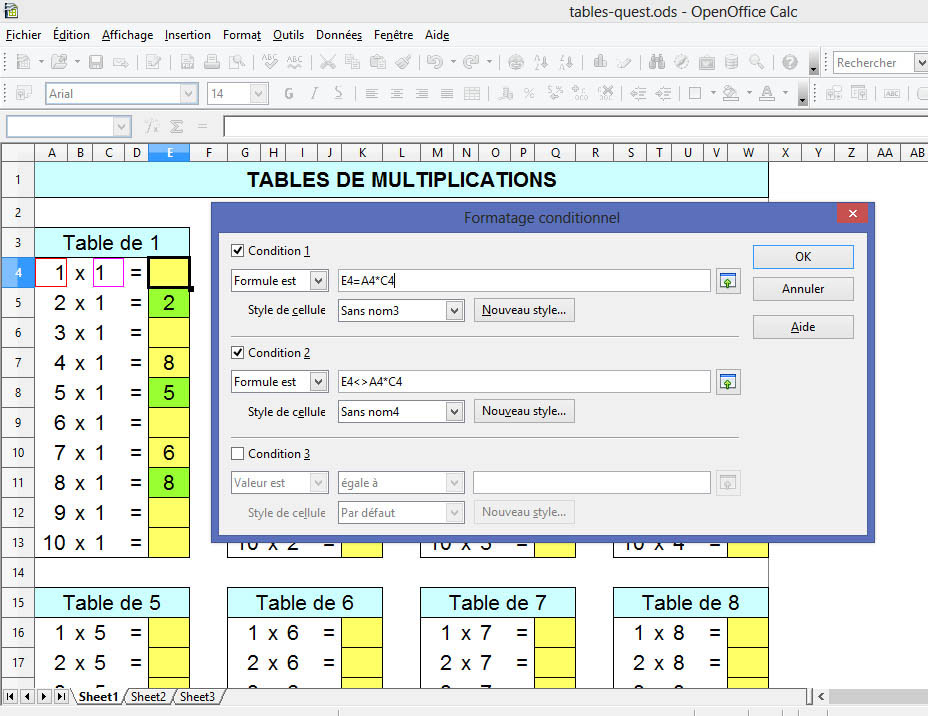
TABLES de MULTIPLICATION avec OPEN OFFICE CALC

La résolution du problème avec Open Office Calc se fait de manière un peu différente: Toutes les tables sont affichées mais sans le résultat. L'utilisateur entre le résultat d'une multiplication dans la case orangée. Si le résultat est juste la case devient verte dans le cas contraire la case reste orange. Ceci est réalisé avec le formatage conditionnel.

Cliquer sur l'image pour agrandir

Pile ou face

Principe: Compter combien de piles et de faces apparaissent en N lancers de pièce. Vérifier , lorsque le nombre de lancers est grand que les probabilités d'apparition tendent vers 1/2. Cet exercice est bien à faire faire par des 3ème qui s'initient aux probabilités sous la forme d'observation.
Description de l'algorithme: L'utilisateur choisit le nombre N de tirages. Une boucle permet de compter le nombre de piles et le nombre de faces. Afficher le résultat sous forme de fréquence (rapport du nombre d'apparition d'une face sur le nombre total de lancers).

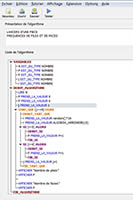
ALGORITHME - PILE ou FACE

Sous ALGOBOX, c'est la fonction ALGOBOX_ALEA_ENT(1,10) qui permet de générer un nombre aléatoire entre 1 et 10. Les 5 premières valeurs sont attribuées au "pile" et les 5 autres aux "faces". On peut faire plus simple avec ALGOBOX_ALEA_ENT(0,1).

Cliquer sur l'image pour agrandir

Faire un clic-droit et utiliser l'option "enregistrer sous" pour télécharger le fichier.

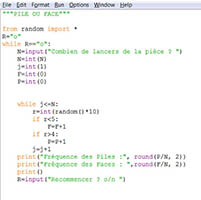
PROGRAMME PYTHON - PILE ou FACE

Sous Python, c'est la fonction random qui permet de générer un nombre aléatoire.

Cliquer sur l'image pour agrandir

TABLES de MULTIPLICATION avec OPEN OFFICE CALC

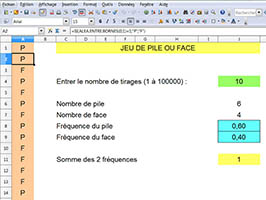
La résolution du problème avec Open Office Calc se fait de manière un peu différente: Toutes les valeurs pile (P) ou face (F) sont affichées (ici jusqu'à 1500 mais on peut aller plus loin en étirant la formule). L'utilisateur entre le nombre de lancers qu'il souhaite. Un indexage permet de compter le nombre de piles et le nombre de faces (voir la formulation sur l'image 2 agrandie).

Cliquer sur l'image pour agrandir (2 images)

Des poules et des lapins

Problème 1: Dans la cour d'une ferme, il y a des poules et des lapins. J’ai compté 16 têtes et 44 pattes. Combien y a-t-il de poules ? Combien y a-t-il de lapins ? Ça y est, je vous vois venir: vous allez me dire qu'il est plus simple de faire le calcul (en tâtonnant ou avec un système de deux équations à deux inconnues si on est allé jusqu'en 3ème) que d'écrire un programme. Bon, comme vous allez le constater le programme est très simple et très court et de plus je rajoute deux problèmes avec des données de départ différentes et là on commence à comprendre pourquoi faire un programme est intéressant:

Problème 2 : Dans la cour d'une ferme, il y a des poules et des lapins. J’ai compté 91 têtes et 234 pattes. Combien y a-t-il de poules ? Combien y a-t-il de lapins ?
Problème 3 : Dans la cour d'une ferme, il y a des poules et des lapins. J’ai
compté 2171 têtes et 4368 pattes. Combien y a-t-il de poules ? Combien y a-t-il de lapins ? ... et je pourrais en rajouter encore beaucoup. L'idée est de faire un programme qui serve à toutes les situations et vous permettra même d'en créer d'autres. Ce genre de problème est souvent donné dans les rallyes maths dans les classes élémentaires et au collège. Pour trouver la solution en tâtonnant, il est impératif de la structurer sa pensée et c'est ce que fait également l'écriture de l'algorithme.

Description de l'algorithme: L'utilisateur entre le nombre de têtes et le nombre de pattes (cela permet une plus grande flexibilité si l'on veut changer les données par la suite).
Une boucle de 1 jusqu'au nombre de têtes compte le nombre de pattes. Dès que l'on tombe sur le nombre de pattes demandé, on sort de la boucle en affichant les résultats.

Cliquer sur l'image pour agrandir

Faire un clic-droit et utiliser l'option "enregistrer sous" pour télécharger le fichier.

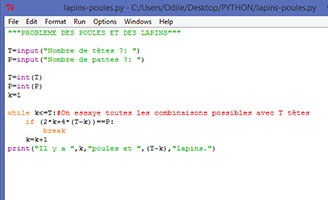
PROGRAMME PYTHON - POULES ET LAPINS
Le programme est très simple, il ne comporte qu'une seule boucle. On essaye toutes les solutions possibles et l'on sort de la boucle dès que la solution est trouvée.

Cliquer sur l'image pour agrandir

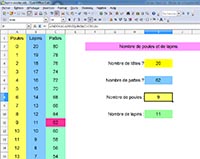
POULES ET LAPINS avec OPEN OFFICE CALC

La résolution du problème avec Open Office Calc se fait de manière un peu différente et il est un fait qu'un tableur n'est pas ici la solution la plus appropriée pour ce genre de problème. Comme précédemment, l'utilisateur entre le nombre de têtes et le nombre de pattes. La première colonne affiche le nombre de poules, une deuxième colonne le nombre de lapins de telle sorte que la somme des deux nombres sur une même ligne est égale au nombre de têtes. Une troisième colonne affiche le nombre de pattes pour chaque possibilité, c'est à dire pour chaque ligne. Avec la formule EQUIV, i est possible de rechercher dans cette colonne le nombre de pattes qui a été demandé au départ. Cela fournit un INDEX pour la colonne des poules et la colonne des lapins, donc la solution. J'ai rajouté un formatage conditionnel sur la colonne du nombre de pattes pour que la solution s'affiche en rose.

LE PROF 2.0
Mentions légales